آموزش حل گرهای حل معادلات ode در نرم افزار متلب و سیمولینک
بسیاری از محققین و دانشجویان از نرم افزار متلب برای حل معادلات ordinary differential equation یا ode استفاده می کنند. برای حل معادلات ode نرم افزار متلب حل گرهای متفاوتی را در اختیار کاربران قرار میدهد. در این پست هدف بررسی حل گرهای معادلات ode و آموزش استفاده از حل گرها و حل معادلات به کمک آنها است. در ابتدا حل گر به صورت عمومی توضیح داده شده و سپس هر کدام از آپشن ها و خصوصیات مختلف دستور توضیح داده شده است.
در صورت داشتن هرگونه سوال، لطف کنید سوالاتتون رو در قسمت نظرات مطرح کنید. و در صورت داشتن پروژه در خصوص نرم افزار MATLAB و مهندسی مکانیک ، کنترل، محاسبات عددی، SIMULINK، SimMechanics میتوانید از طریق ایمیل و تلفن در قسمت تماس با ما، ارتباط برقرارکنید.
حل گرهای معادلات ode در نرم افزار متلب

دستور اصلی نرم افزار متلب برای حل معادلات فوق به صورت زیر است.
[T,Y] = solver(odefun,tspan,y0,options)
Solver : در ابتدا به بررسی solver که معرف انواع حل گرها است پرداخته میشود. همانگونه که مشخص است برای حل معادلات ode در نرم افزار متلب باید به جای solver یکی از حل گر های ode23, ode45, ode113, ode15s, ode23s, ode23t, and ode23tb قرار داده شود. برای مثال برای حل معادلات با حل گر ode45 که حل گر عمومی نرم افزار متلب است به صورت زیر عمل میشود. هر کدام از حل گر ها دارای تواناییهای متفاوتی هستند که در پست های آتی به طور مفصل مورد بررسی قرار خواهند گرفت.
[T,Y] = ode45(odefun,tspan,y0,options)
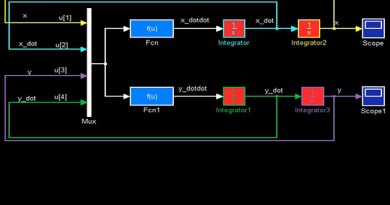
Odefun: نام تابعی است که قرار است مورد حل قرار بگیرد برای حل هر تابع دلخواه باید آن را به فرم استاندارد در آورد. فرم استاندارد فرمی است که کلیه مرتبه های بالاتر از یک به مرتبهی یک و پایین تر تبدیل می شوند. در پست … و همچنین در شکل زیر نحوه ی استاندارد سازی یک معادله ی ساده نشان داده شده است.
پس از استاندارد سازی تابع باید آن را به فرم تابعی نوشت که برای حل گرهای متلب قابل استفاده باشد.برای مثال تابع زیربرای معادله ی مرتبه ی دوم به فرم استاندارد نوشته شده است. که با نام دلخواه odefun1 ذخیره شده است.
function dy = odefun1 (t,y)
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = 1000*(1 – y(1)^2)*y(2) – y(1);
end
Tspan: این پارامتر مربوط به زمان شبیه سازی معادله است و به صورت یک بردار دو پارامتری است برای مثال میخواهیم زمان حل معادله بین 0 تا 2 ثا نیه باشد. مقدار tspan=[0,2] قرار داده می شود.
y0: مربوط به شرایط اولیه برای شروع شبیه سازی است. که یک بردار است که به اندازه ی پارامترهای حالت تابع اصلی یا odefun است برای مثال برای تابع odefun1 که در بالا توضیح داده شد مقدار y0 یک بردار مرتبه ی دو است.
Options: یکی از ویژگی های مهمی که در حل مسائل ode بسیار اهمیت دارد این ویژگی است.که برای استفاده از ان از دستور odeset استفاده می شود. با استفاده از این ویژگی میتوان مشخصاتی از قبیل بیشترین گام حل و مقدار اولیه گام حل و پارامترهای نظیر تلورانس مطلق(برداری هم مرتبه با تعداد متغیر حالت) یا تلورانس نسبی(یک عدد) و سایر مشخصات مروبط به حل حل گر را تغییر داد. برای مثال اگر بخواهیم از حلگری با بیشترین گام0.01 و گام اولیه ی 0.001 استفاده شود و تلورانس نسبی 0.001 و تلورانس مطلق مشابه ایجاد کینیم ین تغییرات به صورت زیر اعمال می شود.
options = odeset(‘InitialStep’,0.001,’MaxStep’,0.001,’RelTol’,.001,’AbsTol’,[0.001 .001]);
در نهایت دو مثال از روش استفاده از حل گر در دو کد مجزا نوشته خواهد شد.
مثال اول
%% ======================Example1==================================
function solve_ode
tspan=[0 3000]
y0=[2,0]
[T,Y] = ode15s(@vdp1000,tspan,y0);
plot(T,Y(:,1),’-o’)
function dy = vdp1000(t,y)
dy = zeros(2,1); % a column vector
dy(1) = y(2);
dy(2) = 1000*(1 – y(1)^2)*y(2) – y(1);
end
end
مثال دوم
%% ======================Example2==================================
function ode_2
options = odeset(‘RelTol’,1e-4,’AbsTol’,[1e-4 1e-4 1e-5]);
[T,Y] = ode45(@rigid,[0 12],[0 1 1],options);
plot(T,Y(:,1),’-‘,T,Y(:,2),’-.’,T,Y(:,3),’.’)
function dy = rigid(t,y)
dy = zeros(3,1); % a column vector
dy(1) = y(2) * y(3);
dy(2) = -y(1) * y(3);
dy(3) = -0.51 * y(1) * y(2);
end
end
|
|||||||||||||||||||||||||||||||||||
در صورت داشتن هرگونه سوال، لطف کنید سوالاتتون رو در قسمت نظرات مطرح کنید. و در صورت داشتن پروژه در خصوص نرم افزار MATLAB و مهندسی مکانیک ، کنترل، محاسبات عددی، SIMULINK، SimMechanics میتوانید از طریق ایمیل و تلفن در قسمت تماس با ما، ارتباط برقرارکنید.



سلام
اگر امکانش هست در مورد ode event هم توضیح بدید
سلام. در اولین فرصت توضیحاتی در همین قسمت میدم.
سلام وقت ب خیر من تو کد نویسی متلب برای تمرین زیر مشکل دارم ممنون میشم کمکم کنید
dx/dt=-2x(t) + t x(0)=1
پاسخ x(t) را برای مدت زمان t=[1,10] ثانیه رسم کنید…
لطفا کمکم کنید باید تا آخر همین هفته ارائه بدم
ممنون
سلام. من به طور کامل توی پست مربوط به حل معادلات ODE توضیح دادم و مسئله ای که برای مثال حل کردم از مسئله ی شما خیلی پیچیده تره.لطف کنید با دقت مطالعه بفرمایید قطعا کمکتون میکنه.
سلام وقت بخیر
من توی حل و رسم دستگاه معادلات دیفرانسیلی زیر گیر کردم اگر ممکنه راهنماییم کنید
da/dt=15((a/15)(1-a/15)-2/(0.6*15))
db/dt=100(α(a/15)^2*(1-b/100)-(0.1/(.6*15)))
dh/dt=110(0.4/0.6)(h/110)(1-h/110)-(15/0.6*15))
ممنون
سلام در پست مربط به حل معادلات ode کامل توضیح دادم. اگه توضیحات بیشتری میخواید لطفا مسئله ر ایمیل کنید
سلام
امکانش هست میراگر MR را با روش ode45 (سیمولینک نه) مدلسازی کنید و در گروه قرار بدید؟؟
متشکرم
سلام . معادلات رو بنویسید تا مورد بررسی قرار بدیم.
اما احتمال زیاد این کار امکان پذیر است. اصولا تابع ode45 رو برای تمام معادلات ordinary میتوان استفاده کرد.
سلام..ببخشید من مي خوام بازه ی زمانیم بزرگ تر 5 باشه اما ODE45 قبول نمي کنه بايد چيکار کنم
برای ode45 فرقی نمیکنه شما میتونید هر بازه زمانی بدین. ممکنه تابع شما بعد از اون بازه زمانی جواب هاش ناپایدار بشن. اما برای ode بازه زمانی اهمیتی نداره و حل میکنه. احتمالا در نحوه ی نوشتن دستور دچار مشکل هستید.
سلام نشانی های ایمیل ها تغییر کردند؟
سلام خیر ولی بهتر است با ایمیل [email protected] در تماس باشید.
با سلام
اگر یک مدار شامل مقاومت سلف و خازن داشته باشیم
از کدام ode ها استفاده می شود
با سلام.
خوب بیشتر حل گرها قابل استفاده هستند. اما فک میکنم ODE45 مناسب باشه
سلام.
مسئله من در مورد معادله ارتعاشی تیر با تحریک بار گسترده رندوم می باشد. من معادله رو بدست اوردم ولی در اعمال بار رندوم به مسئله دچار مشکل شدم. به چه شکلی بار رو به معادله اعمال کنم وبا ode 45 در متلب حل کنم؟؟؟؟؟؟
یه سوال دیگه هم داشتم،
بعد ازحل با ode45 و به دست اوردن پاسخ، باید ماتریسهای m,k رو از روی پاسخ مسئله بدست بیاورم، لطفا در این مورد هم راهنمایی بفرمایید
(ایا باید از پاسخ بدست امده fftبگیرم؟؟؟؟؟؟)
ممنون
تا اونجایی که من میدونم شما بعد از بدست آوردن معادله ابتدا ماتریس ضرایب رو مشخص میکنید و سپس با استفاده از این حلگر پاسخ زمانی رو بدست میارید.