آموزش ترسیم نمودارهای سه بعدی و سطوح در نرم افزار MATLAB
در این پست به آمورش ترسیم نمودارهای سه بعدی در نرم افزار MATLAB پرداخته میشود. قبل از مطالعه ی این پست پیشنهاد می شود که پست 45 را که در آن آموزش ترسیم نمودارهای دو بعدی است مطالعه بفرمایید. بدلیل اینکه مشخصات مربوط به نمودارها و آپشن ها مشابه قبل است و فقط توضیحات پیرامون نمودارهای سه بعدی آورده خواهد شد. به عبارتی این پست به همراه پست 45 تکمیل کننده مطالب مربوط به تسیم نمودارها است. در پست پیشین ترسیم نمودارها به کمک دستور plot با همه جزئیات و مشخصات و آپشن ها آورده شده بود و در این پست دو دستور plot3 , Surf توضیح داده خواهد شد.جهت مشاهده ی این آموزش و دانلود کد MATLAB نوشته شده به ادامه مطلب مراجعه نمایید.
آموزش ترسیم نمودارهای سه بعدی و سطوح در نرم افزار MATLAB
قبل از مطالعه ی این پست بهتر است پست پیش نیاز آن که مربوط به ترسیمات دوبعدی و مشخصات نمودارها است را مطالعه نمایید.
1. ترسیم خطوط سه بعدی
خطوط سه بعدی در حالت کلی دارای معادله ی 0=(f(x,y,z هستند که در حالت پارامتری بر حسب متغیر وابسته ی t هم نوشته میشودند.
x=x(t)
y=y(t)
z=z(t)
البته این مشخصات میتوانند مشخصات خطوط دو بعدی هم باشد که با توجه به تعریف صفحه ی بوسان میتوان تشخیص داد که این مشخصات مربوط به خطوط دو بعدی یا سه بعدی هستند.
در این قسمت میخواهیم یک مثال از ترسیم این خطوط را به کمک نرم افزار MATLAB انجام دهیم.
مثال زیر را ترسیم کنید.
x=sin(t)
y=cos(t)
z=t
حل:
در ابتدا بردار مستقل t تعریف میشود. نحوه ی تعریف برداردها در این پست به طور کامل توضیح داده شده است.
t = 0:pi/50:10*pi;
پس از تعریف متغیر مستقل متغیرهای وابسته به صورت زیر تعریف میشوند.
x=sin(t);
y=cos(t);
z=t;
و در نهایت دستور ترسیم نوشته میشود.
plot3(x,y,z);
و همچنین آپشن های مربوط در نمودار که پیشتر توضیح داده شده است اضافه شده است.
xlabel(‘sin(t)’)
ylabel(‘cos(t)’)
zlabel(‘t’)
grid on
axis square
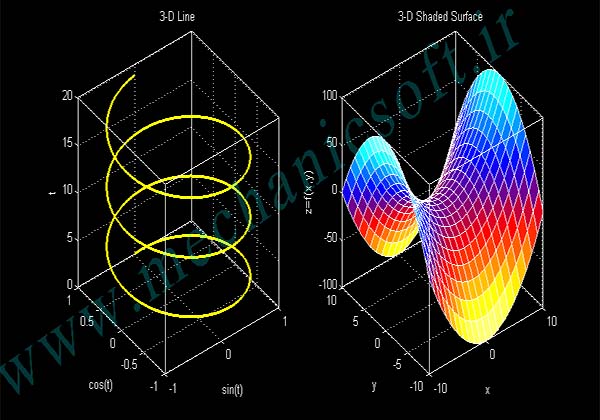
در عکس پایین صفحه فرم کلی دستور به همراه نمودار ترسم نشان داده شده است.
2. ترسیم سطوح
سطوح در حالت کلی دارای معادله ی (z=f(x,y هستند. برای نشان دادن ترسیم سطوح نیز مثال زیر را در نرم افزار MATLAB بررسی میکنیم.
شکل حاصل از معادله ی z=y^2-x^2 را در نرم افزار MATLAB ترسیم نمایید.
برای ترسیم این عبارت ابتدا باید دو بردار x و y تشکیل شود .
xx=-10:1:10;
yy=-10:1:10;
پس از تشکیل این دو عبارت باید هر نقطه ی x با تمام نقاط y متناظر شود که از دستور زیر استفاده میشود.
[x,y]=meshgrid(xx,yy);
پس از ایجاد نقاط متناظر میتوان به راحتی معادله ی مورد نظر را به صورت زیر نوشت.
z=x.^2-y.^2;
سپس با کمک دستور surf صفحه ی مورد نظر را ترسیم کرد.
surf(x,y,z)
سایر تنظیمات دیگر هم در پست 45 توضیح داده شده است که بر خی از آنها در زیر آورده شده است.
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z=f(x,y)’)
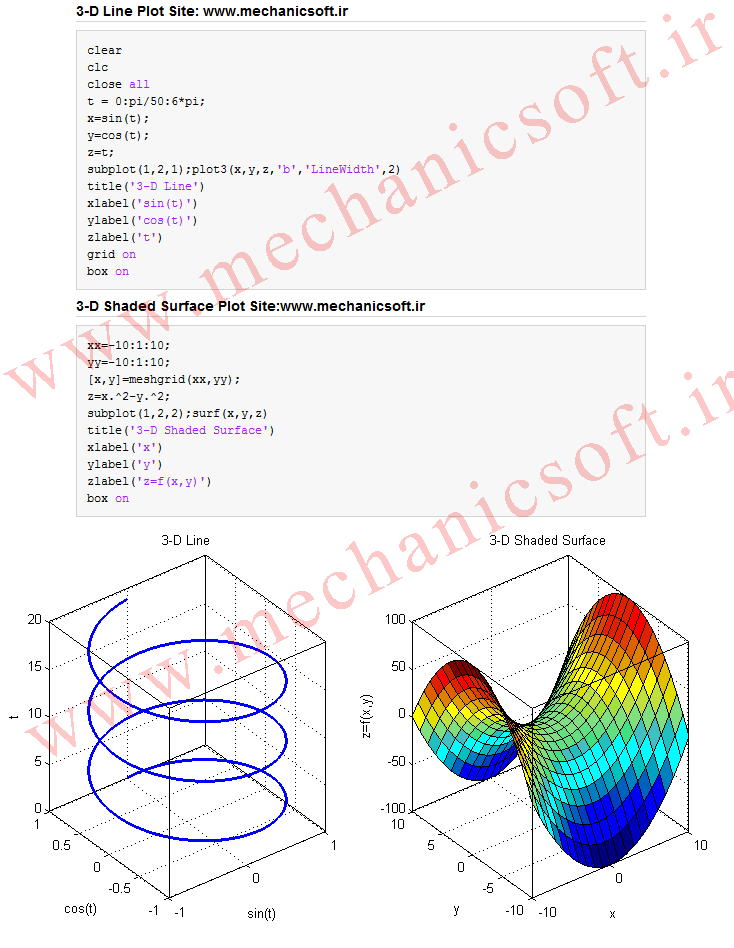
شکل کلی دستورات به همراه شکل های ترسیم شده در شکل زیر نشان داده شده است.
%% 3-D Line Plot Site: www.mechanicsoft.ir
clear
clc
close all
t = 0:pi/50:6*pi;
x=sin(t);
y=cos(t);
z=t;
subplot(1,2,1);plot3(x,y,z,’b’,’LineWidth’,2)
title(‘3-D Line’)
xlabel(‘sin(t)’)
ylabel(‘cos(t)’)
zlabel(‘t’)
grid on
box on
%% 3-D Shaded Surface Plot Site:www.mechanicsoft.ir
xx=-10:1:10;
yy=-10:1:10;
[x,y]=meshgrid(xx,yy);
z=x.^2-y.^2;
subplot(1,2,2);surf(x,y,z)
title(‘3-D Shaded Surface’)
xlabel(‘x’)
ylabel(‘y’)
zlabel(‘z=f(x,y)’)
box on
جهت داشتن هر گونه سوال، مشاور، درخواست هر گونه پروژه کدنویسی با نرم افزار متلب به ارتباط با ما مراجعه نمایید.
![mechanicsoft[dot]ir](http://www.mechanicsoft.ir/wp-content/uploads/2015/10/mechanicsoftdotir.png)


مرسی از توضیحتون