آموزش سریع نرم افزار متلب در یک پست
آموزش سریع نرم افزار متلب در یک پست
آموزش سریع نرم افزار متلب در یک پست : از آنجایی که نرم افزار متلب یک نرم افزار کاربردی و بسیار مهم در زمینه ی برنامه نویسی و محاسبات عددی برای مهندسین است. تصمیم داریم در این پست تا انتها مباحث مهم و کاربردی MATLAB را در اختیار دوستان قرار دهیم. تمام تلاشم این است که مطالب تا جای ممکن کامل باشد، و طوری که باشد که یک نفر که با مطلب آشنایی ندارد بتواند تا حد بسیار خوبی این نرم افزار را یاد بگیرد. بهتون قول میدم بعد از مطالعه این پست مطالب مفید زیادی از نرم افزار متلب یاد گرفته باشید. لطفا نظرات و سوالات خودتون رو در قسمت نظرات پایین پست مطرح بفرمایید تا در اسرع وقت جواب داده بشه.
معرفی نرم افزار MATLAB
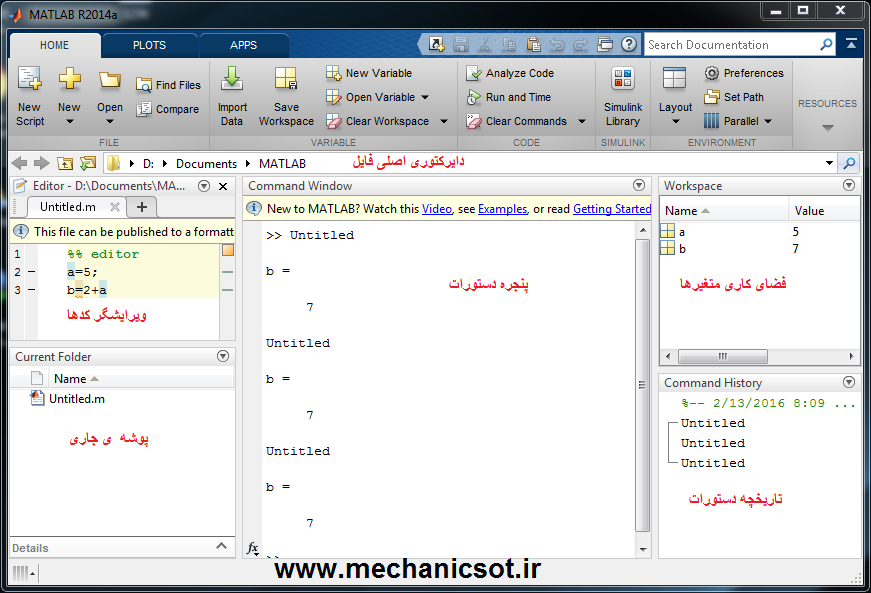
در شکل زیر محیط نرم افزار متلب و قسمت های اصلی آن نشان داده شد است. دایرکتوری اصلی مربوط به پوشه ی اصلی است که کدهای متلب در آن ذخیره و اجرا می شود. پنجره ی دستورات پنجره ی نمایش خروجی کدهای نوشته شده در ویرایشگر و همچنین نوشتن دستورات و گرفتن خروجی است. پوشه ی جاری پوشه و فایل های نرم افزار متلب است که ذخیره شده است. فضای کاری متغیرها، فضای کاری است که بعد از مقدار دهی به متغیری در آن نمایش داده می شود و تاریخچه ی دستورات کلیه دستورات اجرا شده در پنجره ی دستورات را در خود نگه می دارد.
آموزش سریع نرم افزار متلب در یک پست : نرم افزار متلب به عنوان یک ماشین حساب
از پنجره ی دستورات نرم افزار متلب می توان به عنوان یک ماشین حساب استفاده کرد. برای مثال در نرم افزار متلب می توان چهار عمل اصلی را به راحتی انجام داد.
| >> 1+2*3 ans = 7 |
در صورتی که در هنگام محاسبات مقداری به متغیر داده نشود خروجی در مقدار ans ذخیره می شود. اما در صورتی که مقدار دهی شود مقدار خروجی در آن ذخیره می شود.برای مثال در مثال زیر محاسبات فوق به متغیر x اختصاص داده شده است
| >>x= 1+2*3 x = 7 |
عملگرای زیر عملگرهای اصلی نرم افزار متلب هستند. نکته ی قابل توجه ترتیب و اولویت عملگرها است که ابتدا اولیت با پرانتز است پس از آن عملگر توان^ سپس عملگر ضرب و تقسیم و پس از آن عملگر جمع و تفریق هستند.
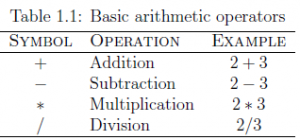
در این خصوص توجه هات ر ا به دو مثال های زیر جلب می کنم
| >> (1+2)*3 ans = 9 |
در مثال بالا ابتدا پرانتز عمل میکند و سپس عملگر ضرب چون اولویت با پرانتز است
| >> 1+2*3 ans = 7 |
در مثال قبل نیز ابتدا عملگر ضرب عمل می کند و پس از آن عملگر جمع پس ضرب دو در سه می شود شش و پس از آن با یک جمع می شود که حاصل کل مقدار هفت شده است.
در مثال زیر اول اولویت با پرانتز است و پس از آن با علامت توان و بعد از آن با ضرب و تقسیم در نهایت علامت جمع
| >> 1/(2+3^2)+4/5*6/7 ans = 0.7766 |
مقدار دهی به متغیر در متلب
در نرم افزار متلب مقدار دهی به متغیر با علامت = انجام میگیرد . این علامت به معنی عبارت منطقی تساوی نیست بلکه برای مقداردهی استفاده می شود. بعلاوه اگر به یک مقدار عددی خاص داده شد. و پس از ان آن مقدار عوض شد مقدار جدید جایگزین مقدار قبلی می شود. دستور زیر را در مطل تایپ و خروجی را چک کنید.
| >> t = 5; >> t = t+1 t = 6 |
در صورتی که دستوری به درستی اجرا نشود در نرم افزار متلب با دستور خطا مواجه می شودید. در مثال زیر علامت ضربدر* بین دو عبارت قرار داده نشده است همانطور که مشاهده میکنید با پیغام خطا روبرو شده ایم
| >>x = 10; >> 5x ??? 5x | Error: Unexpected MATLAB expression. |
توابع معروف در نرم افزار متلب
در راستای آموزش سریع نرم افزار متلب در یک پست در این قسمت به بررسی متغیرهای مقدار دهی شده در نرم افزار متلب کافی است که از دستور who استفاده شود.
نرم افزار متلب بسیار از توابع معروف را می شناسد که در زیر برخی از آنها نام برده و مثال زده می شود.
آموزش سریع نرم افزار متلب در یک پست(جدول مربوط به توابع مثلثاتی)
| تابع | دستور متلب |
| توابع مثلثاتی (رادیان) | sin() cos() tan () |
| معکوس توابع مثلثاتی | asin() acos() atan () |
| توابع مثلثاتی (درجه) | sind() cosd() tand () |
| توابع هایپربولیک | sinh() cosh() tanh () |
| معکوس توابع هایپربولیک | asinh() acosh() atanh () |
| تابع اکسپونسشیال | exp() |
| ال ان- لگاریتم در مبنای عدد نپر | log() |
| تابع لگاریتم در مبنای ده | log10() |
| قدرمطلق | abs() |
| رادیکال | sqrt() |
توابع فوق برخی توابع روتینی هستند که دائم استفاده می شوند. توابع دیگری هم هستند که اکنون حضور ذهن ندارم دوستان در نظرات یاداوری کنند تا تکمیلش کنیم.
در قسمت زیر چند مثال از توابع آورده شده است.
| >> sin(60*pi/180) ans =0.8660
>> sind(60) ans =0.8660 >> cosh(0) ans =1 >> log10(100) ans =2 >> log(exp(5)) ans =5 >> exp(sind(60)^2) ans =2.1170 |
ایجاد بردار در نرم افزار متلب
در این قسمت به اموزش ایجاد بردار در نرم افزار متلب پرداخته شده است. بردارهای یکی از مطالب بسیار مهم و کاربردی در نرم افزار متلب هستند.
روش اول ایجاد بردار در MATLAB:
میخواهیم برداری ایجاد کنیم که مقدار اولیه ی آن ۱۰- و مقدار نهایی آن ۱۰+ است
| >>x=[-10,-9,-8,-7,-6,-5,-4,-3,-2,-1,0,1,2,3,4,5,6,7,8,9,10] |
ساده ترین روش ایجاد بردار در مطلب به صورت فوق است اما یک ایراد بزرگ دارد و آن هم وقتی است که تعداد اعضای بردار زیاد میشود.
روش دوم ایجاد بردار در MATLAB:
|
x= انتهای بازه : مقدار گام : ابتدای بازه ; x=-10:1:10; |
در این روش ما آمدیم و از ۱۰- شروع کرده و یکی یکی اضافه کردیم تا به ده رسیدیم این یکی از ساده ترین روشهای ایجاد بردار در نرم افزار MATLAB است.
روش سوم ایجاد بردار در MATLAB:
|
x=linspace(تعداد اعدادی که میخواهیم در این بازه داشته باشیم,انتهای بازه ,ابتدای بازه); x=linspace(-10,10,21); |
در این روش بردار بر اساس مقدار ابتدا و انتها و اعدادی که در بین آنها قرار میگرد ایجاد میشود .یعنی برداری میخواهیم که ابتدای آن ۱۰- و انتهای آن ۱۰+ باشد و بعلاوه از ۱۹ عدد که با دو مقدار ابتدا وانتها میشود ۲۱ عدد هم تشکیل شده باشد
عملگر نقطه “.” در نرم افزار MATLAB
هر گاه این عملگر قبل از ضرب و تقسیم و توان بیاید برروی هر کدام از اعضای بردار به طور جداگانه اعمال میشود.
برای مثال ما هیچ گاه نمیتوانیم یک بردار مثل بردار شکل زیر را به توان ۲ برسانیم امابه کمک این عملگر میتوانیم هر کدام از اجزای آن را به توان ۲ برسانیم.
دو بردار زیر را در نظر بگیرید.
| d1=[1 2 3 4];
d2=[-1 1 -4 4]; |
اگر یکی از بردارها را به توان برسانیم با پیغام خطا مواجه خواهیم شد
| d1^2; #Error |
دلیل این خطا این است که هیچ گاه نمیتوان یک بردار را به توان رساند. اما برای هر کدام از اعضای آن میتوان این کار را کرد. که این کار با قرار دادن عملگر نقطه قبل از توان انجام می شود.
| >>g=d.^2; ==> خروجی دستور==> g=[1 4 9 16] |
از لحاظ منتطقی هیچ گاه نمیتوان دو بردار دلخواه را در هم ضرب کرد. برای مثال ضرب زیر به شما خطا میدهد.
| >>g1=d1*d2 #Error |
اما میتوان هر ارایه ی نظیر یک بردار را در ارایه ی نظیر بردار دیگر ضرب کرد که این کار با ضرب نقطه ای انجام میشود.یعنی یک نقطه قبل از ضرب قرار میگیرد.
| >>g2=d1.*d2 ==> خروجی دستور==> g2=[-1 2 -12 16] |
ترسیم نمودارهای دو بعدی در متلب
دراین قسمت از آموزش سریع نرم افزار متلب در یک پست بصورت بسیار ساده ترسیمات دو بعدی درنرم افزار متلب آموزش داده شده است.
بعد از یادگیری مفهیم فوق با یک مثال ساده شروع میکنیم.
ترسیم تابع زیر در بازه ی ۱۰- تا ۱۰+
y=sin(50*x)+0.01*x^3;
ابتدا تابع ایکس را به تعدا تقسیمات لازم در بازه ای که نیاز داریم ایجاد میکنیم
| >>x=-10:1:10; |
پس از آن متغیر وابسته ی y را به صورت بردار و با استفاده از “عملگر نقطه” در هر جا که لازم باشد ایجادمیکنیم
| >>y=sin(50.*x)+(0.01).*x.^3; |
به عملگر نقطه قبل از ضرب و توان دقت نمایید.
بعد از آن با استفاده از دستور plot ترسیم انجام خواهد شد.
با استفاد از دستور زیر میتوانید عنوانی برای نمودار انتخاب کنید.
| title(‘your Title’); |
با استفاده از دستور زیر میتوانید نام نمودارهای عمودی و افقی را به صورت دلخواه قرار دهید.
| xlabel(‘Time’); ylabel(‘Displasement’); |
با استفاده از دستور زیر میتوانید برچسبی برای نمودار ایجاد کنید
| legend(‘blue’); |
با استفاده از این دستور میتوانید هر متنی را در هر نقطه ی دلخواه از نموار بنویسید.
| text(-6,6,’ \uparrow www.mechanicsoft.ir’,’FontSize’,18); |
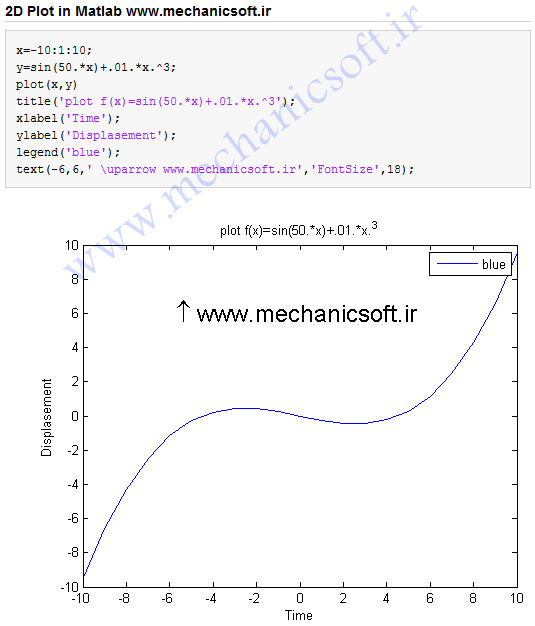
در پایان این قسمت مجموعه ی دستورات به همراه خروجی متلب به صورت زیر است.
| %% ۲D Plot in Matlab www.mechanicsoft.ir x=-10:1:10; y=sin(50.*x)+.01.*x.^3; plot(x,y) title(‘plot f(x)=sin(50.*x)+.01.*x.^3’); xlabel(‘Time’); ylabel(‘Displasement’); legend(‘blue’); text(-6,6,’ \uparrow www.mechanicsoft.ir’,’FontSize’,18); |
ترسیم مسیر و سطوح سه بعدی در نرم افزار متلب
در این قسمت از آموزش سریع نرم افزار متلب در یک پست به ترسیم سطوح و مسیرهای سه بعدی پرداخته شده است.
1.ترسیم مسیر
خطوط سه بعدی در حالت کلی دارای معادله ی ۰=(f(x,y,z هستند که در حالت پارامتری بر حسب متغیر وابسته ی t هم نوشته میشودند.
x=x(t)
y=y(t)
z=z(t)
البته این مشخصات میتوانند مشخصات خطوط دو بعدی هم باشد که با توجه به تعریف صفحه ی بوسان میتوان تشخیص داد که این مشخصات مربوط به خطوط دو بعدی یا سه بعدی هستند.
در این قسمت میخواهیم یک مثال از ترسیم این خطوط را به کمک نرم افزار MATLAB انجام دهیم.
مثال زیر را ترسیم کنید.
x=sin(t)
y=cos(t)
z=t
حل:
در ابتدا بردار مستقل t تعریف میشود. نحوه ی تعریف برداردها در قسمت های قبل به طور کامل توضیح داده شده است.
| t = 0:pi/50:10*pi; |
پس از تعریف متغیر مستقل متغیرهای وابسته به صورت زیر تعریف میشوند.
| x=sin(t); y=cos(t); z=t; |
و در نهایت دستور ترسیم نوشته میشود.
| plot3(x,y,z); |
و همچنین آپشن های مربوط در نمودار که پیشتر توضیح داده شده است اضافه شده است.
| xlabel(‘sin(t)’) ylabel(‘cos(t)’) zlabel(‘t’) grid on axis square |
در عکس پایین صفحه فرم کلی دستور به همراه نمودار ترسم نشان داده شده است.
۲٫ ترسیم سطوح
سطوح در حالت کلی دارای معادله ی (z=f(x,y هستند. برای نشان دادن ترسیم سطوح نیز مثال زیر را در نرم افزار MATLAB بررسی میکنیم.
شکل حاصل از معادله ی z=y^2-x^2 را در نرم افزار MATLAB ترسیم نمایید.
برای ترسیم این عبارت ابتدا باید دو بردار x و y تشکیل شود .
| xx=-10:1:10; yy=-10:1:10; |
پس از تشکیل این دو عبارت باید هر نقطه ی x با تمام نقاط y متناظر شود که از دستور زیر استفاده میشود.
|
[x,y]=meshgrid(xx,yy); |
پس از ایجاد نقاط متناظر میتوان به راحتی معادله ی مورد نظر را به صورت زیر نوشت.
| z=x.^2-y.^2; |
سپس با کمک دستور surf صفحه ی مورد نظر را ترسیم کرد.
|
surf(x,y,z) |
سایر تنظیمات دیگر هم در مطالب پست های قبلی به صورت مفصل توضیح داده شده است که بر خی از آنها در زیر آورده شده است.
| xlabel(‘x’) ylabel(‘y’) zlabel(‘z=f(x,y)’) |
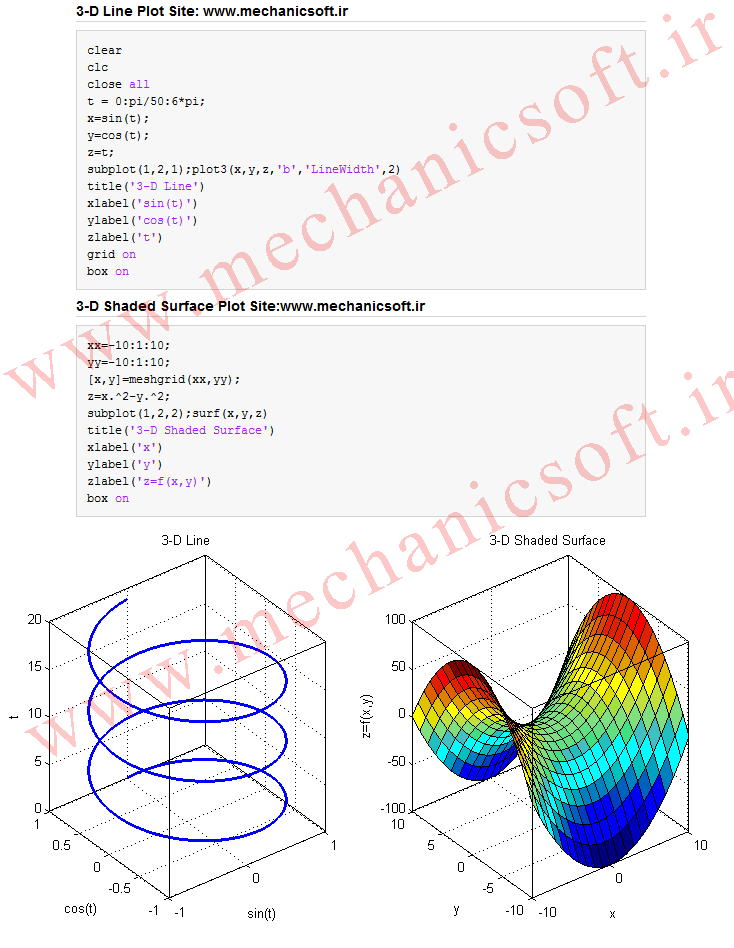
شکل کلی دستورات به همراه شکل های ترسیم شده در شکل زیر نشان داده شده است.
| %% ۳-D Line Plot Site: www.mechanicsoft.ir clear clc close all t = 0:pi/50:6*pi; x=sin(t); y=cos(t); z=t; subplot(1,2,1);plot3(x,y,z,’b’,’LineWidth’,2) title(‘3-D Line’) xlabel(‘sin(t)’) ylabel(‘cos(t)’) zlabel(‘t’) grid on box on %% ۳-D Shaded Surface Plot Site:www.mechanicsoft.ir xx=-10:1:10; yy=-10:1:10; [x,y]=meshgrid(xx,yy); z=x.^2-y.^2; subplot(1,2,2);surf(x,y,z) title(‘3-D Shaded Surface’) xlabel(‘x’) ylabel(‘y’) zlabel(‘z=f(x,y)’) box on |
برنامه نویسی در متلب
در این قسمت از آموزش سریع نرم افزار متلب در یک پست به برنامه نویسی و اصول کنترل جریان برنامه در نرم افزار متلب پرداخته خواهد شد.
این پست ادامه دارد و به زودی تکمیل می شود.
جهت داشتن هر گونه سوال، مشاور، درخواست هر گونه پروژه کدنویسی با نرم افزار متلب به ارتباط با ما مراجعه نمایید.



با سلام و با تشکر از بسیارمطالب خوبتون
جناب دکتر رضایی برای تحلیل structural در انسیس در فشار متغییر چه کاری باید انجام داد ممنون میشم راهنمایی کنید .
تحلیل لوله در فشار متغییر در محیط structural
سلام. خوب باید فشار رو به صورت تابع تعریف کرد. حالا میتونه تابع زمانی باشه یا تابع هر متغیر دیگه ای . فقط اگر که فشار تابع زمانی باشه باید توی محیط transient structural تحلیل بشه. موفق باشید.