آموزش کنترل خطی و مدرن در نرم افزار MATLAB – قسمت اول
آموزش کنترل خطی و مدرن در نرم افزار MATLAB – قسمت اول
همانطور که می دانید کنترل یکی از علوم ترکیبی است که در مهندسی مکانیک و مهندسی برق و مهندسی شیمی کاربرد فراوان دارد. و بعلاوه کنترل یک رشته ی جدا در بسیاری از کشورها محسوب میشود. در این پست و پست های آتی مربوطه هدفمان آموزش مبانی این علم به کمک نرم افزار MATLAB است. پیش نیاز این آموزش آشنایی با درس کنترل کلاسیک دوره ی کارشناسی است. در این پست مفاهیم اولیه کنترل خطی و مدرن را به وسیله ی نرم افزار MATLAB توضیح داده خواهد شد. مفاهیم مربوط به این درس در رابطه با نحوه ی مدل سازی یک تابع تبدیل و سری کردن توابع تبدیل، موازی کردن آنها و محاسبه ی فید بک است.
نحوه ی نوشتن تابع تبدیل در نرم افزار متلب
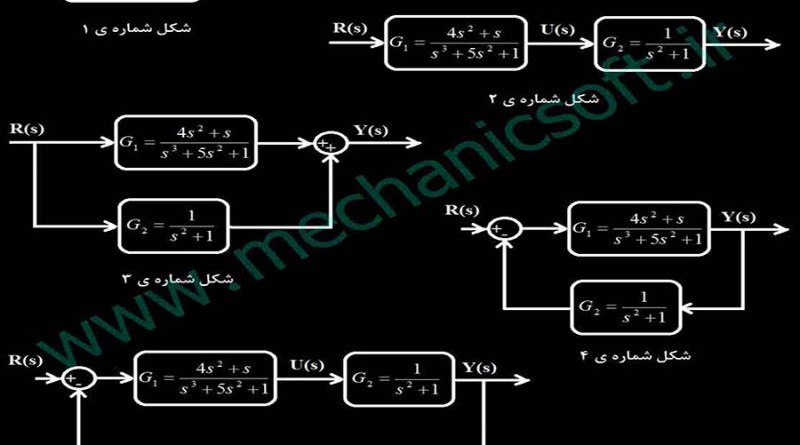
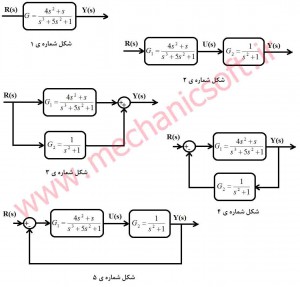
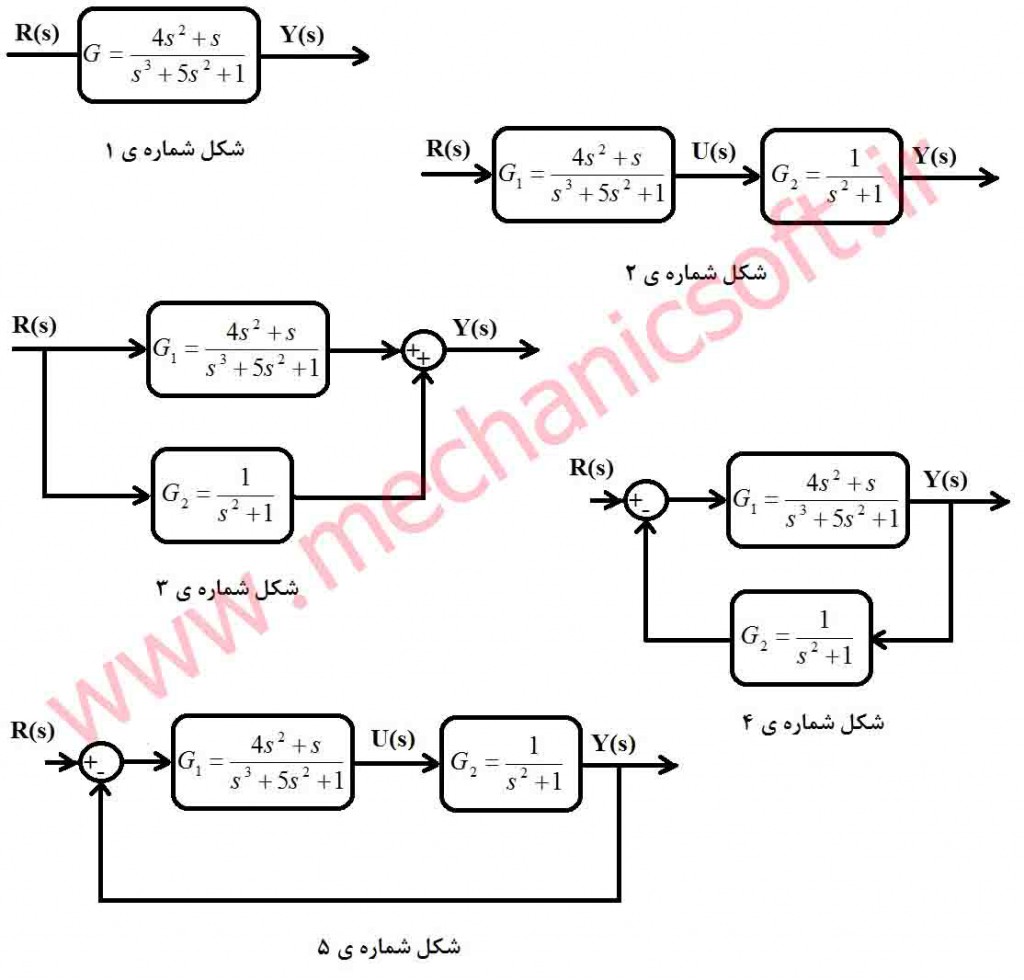
بر اساس شکل های نوشته شده انواع حالت توابع تبدیل را به پنج شکل مختلف نشان داده ایم که هر شکل را بر اساس آن توضیح ونتایج مربوط به آن محاسبه میشود.
بررسی شکل شماره ی یک
در شکل شماره ی 1 یک تابع تبدیل معمولی نوشته شده است نحوه ی نوشتن و نمایش این تابع تبدیل معمولی در نرم افزار متلب به صورت زیر است. پاسخ نهایی به همراه کلیه کدها در عکس در پایان توضیحات قرار داده شده است.
%% Figure 1
numG=[4 1 0]
denG=[1 5 0 1]
sys1=tf(numG,denG)
printsys(numG,denG,’z’)
بررسی شکل شماره ی دو
در این قسمت نحوه ی محاسبه ی دو تابع تبدیل سری نشان داده شده است معمولا هر سیستم کنترلی یک کنترل کننده دارد که به پلنت یا سیستم کنترل نشده متصل می شود لذا این مدل در محاسبات سیستم های کنترل کاربرد فراوان دارد.
%% Figure 2
disp(‘Figure 2′)
numG1=[4 1 0]
denG1=[1 5 0 1]
numG2=[1]
denG2=[1 0 1]
[num,den]=series(numG1,denG1,numG2,denG2)
sys2=tf(num,den)
printsys(num,den,’z’)
بررسی شکل شماره ی سه
در این قسمت نحوه ی محاسبه ی دو تابع تبدیل موازی نشان داده شده است. برای محاسبه ی تابع تبدیل مجموع به صورت زیر عمل می شود.
%% Figure 2
disp(‘Figure 3′)
numG1=[4 1 0]
denG1=[1 5 0 1]
numG2=[1]
denG2=[1 0 1]
[num,den]=parallel(numG1,denG1,numG2,denG2)
sys2=tf(num,den)
printsys(num,den,’z’)
بررسی شکل شماره ی چهار و پنج
در این قسمت نحوه ی محاسبه ی فیدبک توابع با استفاده از دو روش و دستور cloop و feedback نشان داده شده است. در شکل چهار تابع تبدیل فیدبک مقدار دارد و در شکل پنج تابع تبدیل فیدبک مقدار -1 دارد که کدهای آن در نرم افزار متلب به صورت زیر است.
%% Figure 4
disp(‘Figure 4′)
numG1=[4 1 0];
denG1=[1 5 0 1];
numG2=[1];
denG2=[1 0 1];
[num,den]=feedback(numG1,denG1,numG2,denG2)
sys4=tf(num,den)
printsys(num,den,’z’)
%% Figure 5
disp(‘Figure 5′)
numG1=[4 1 0];
denG1=[1 5 0 1];
numG2=[1];
denG2=[1 0 1];
[numS,denS]=series(numG1,denG1,numG2,denG2)
[num,den]=cloop(numS,denS,-1)
sys5=tf(num,den)
printsys(num,den,’z’)
در نهایت خروجی متلب به صورت زیر است.
Figure 1
numG =
4 1 0
denG =
1 5 0 1
Transfer function:
4 s^2 + s
—————
s^3 + 5 s^2 + 1
num/den =
4 z^2 + z
—————
z^3 + 5 z^2 + 1
Figure 2
numG1 =
4 1 0
denG1 =
1 5 0 1
numG2 =
1
denG2 =
1 0 1
num =
0 0 0 4 1 0
den =
1 5 1 6 0 1
Transfer function:
4 s^2 + s
—————————–
s^5 + 5 s^4 + s^3 + 6 s^2 + 1
num/den =
4 z^2 + z
——————————
z^5 + 5 z^4 + z^3 + 6 z^2 + 1
Figure 3
num =
0 4 2 9 1 1
den =
1 5 1 6 0 1
Transfer function:
4 s^4 + 2 s^3 + 9 s^2 + s + 1
—————————–
s^5 + 5 s^4 + s^3 + 6 s^2 + 1
num/den =
4 z^4 + 2 z^3 + 9 z^2 + z + 1
——————————
z^5 + 5 z^4 + z^3 + 6 z^2 + 1
Figure 4
num =
0 4 1 4 1 0
den =
1 5 1 10 1 1
Transfer function:
4 s^4 + s^3 + 4 s^2 + s
———————————-
s^5 + 5 s^4 + s^3 + 10 s^2 + s + 1
num/den =
4 z^4 + z^3 + 4 z^2 + z
————————————
z^5 + 5 z^4 + z^3 + 10 z^2 + z + 1
Figure 5
numS =
0 0 0 4 1 0
denS =
1 5 1 6 0 1
num =
0 0 0 4 1 0
den =
1 5 1 10 1 1
Transfer function:
4 s^2 + s
———————————-
s^5 + 5 s^4 + s^3 + 10 s^2 + s + 1
num/den =
4 z^2 + z
————————————
z^5 + 5 z^4 + z^3 + 10 z^2 + z + 1
>>
در صورت داشتن هر گونه سوال سوالات خود را در قسمت نظرات بنویسید تا در اسرع وقت پاسخ داده شود در ضمن در صورت داشتن هر گونه پروژه صنعتی و دانشگاهی در رابطه با نرم افزار MATLAB و مهندسی کنترل به ایمیل مدیر سایت در بالای سایت قسمت تماس با ما مکاتبه نمایید.

سپاس از تلاشتون . بی نظیر بود